Dalam postingan ini, saya akan membahas algoritma yang termasuk dalam bidang Artificial Intelligence (AI), yaitu Algoritma Genetika. Algoritma genetika adalah bagian dari Evolutionary Computation (EC) yang terinspirasi oleh proses evolusi dan seleksi alam makhluk hidup.

Algoritma genetika umumnya digunakan untuk mengatasi masalah optimasi dan pencarian. Algoritma ini adalah algoritma umum sehingga dapat dengan mudah diimplementasikan dalam berbagai masalah dan dapat memberikan hasil yang lebih baik untuk setiap iterasi dari solusi pencarian. Algoritma genetika dapat menemukan solusi terbaik dari kandidat set yang luas dan memiliki banyak titik optimal dan juga hasilnya cenderung ke optimal global dibandingkan dengan metode serupa seperti hill-climbing, depth-first search, dll.

An Illustrated Guide to Genetic Algorithm

Algoritma genetika dapat digunakan untuk menyelesaikan sejumlah kasus karena kelebihan berikut.

• Terdiri dari banyak solusi prospektif yang dimunculkan sekaligus
• Setiap iterasi menyediakan kandidat untuk solusi yang lebih baik
• Algoritma yang cepat dan efisien

Istilah-istilah dalam Algoritma Genetika

Sebelum kita melangkah lebih jauh, kita harus tahu dulu tentang istilah yang umum digunakan dalam Algoritma Genetika.

• Populasi, kumpulan kemungkinan solusi
• Kromosom, kemungkinan solusi
• Genotype, elemen yang terdapat dalam kromosom
• Fenotype, nilai darigenotype

Selain itu, ada juga istilah lain yang sering digunakan dalam algoritma ini.

• Fungsi fitness, fungsi yang menentukan bobot setiap kromosom
• Nilai fitness, nilai yang diperoleh dari hasil fungsi fitness
• Decoding dan Encoding, dalam beberapa kasus, fenotype dapat diubah ke bentuk lain. Misalnya bilangan biner, real, permutasi, dan integer. Decoding dan encoding adalah proses mengubah satu bentuk ke bentuk lainnya.
• Generasi, jumlah iterasi dalam proses algoritma genetika.

Untuk lebih detail dan contoh penggunaannya, akan saya jelaskan di bagian selanjutnya.

Tahapan-tahapan dalam Algoritma Genetika

Setelah tadi kita mengetahui mengenai keunggulan dan istilah-istilah dalam Algoritma Genetika, sekarang kita akan menggambarkan tahapan-tahapan yang dilakukan oleh algoritma genetika untuk menghasilkan suatu solusi.

Disini, saya akan menjelaskannya tahapan-tahapan tersebut secara umum. Untuk kasus-kasus spesifik, mungkin akan saya jelaskan di artikel selanjutnya.

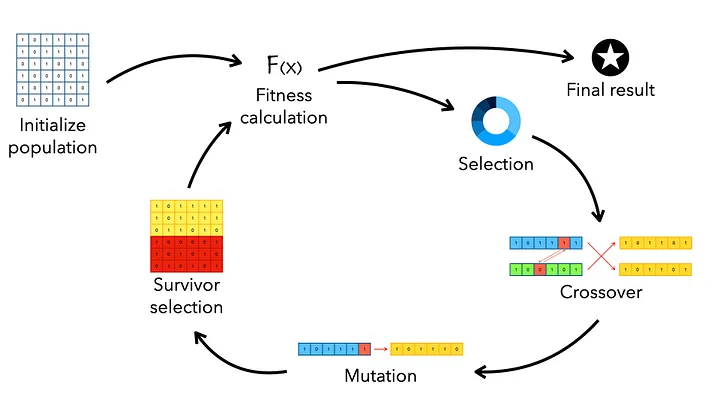
Secara umum algoritma genetika terdiri dari beberapa langkah sebagai berikut.

Inisialisasi populasi

Tahap awal dalam algoritma genetika adalah dengan menginisialisasi populasi. Pada tahap ini kita harus menentukan jumlah populasi dan panjang kromosom yang akan digunakan. Untuk penentuan jumlah populasi sendiri tidak ada ketentuan pastinya. Semakin besar jumlah populasi akan menghasilkan lebih banyak variasi solusi, sehingga memperbesar kemungkinan untuk mencapai solusi terbaik.

Penentuan panjang kromosom biasanya disesuaikan dengan kasus yang ditangani, misalnya jika dalam kasus maksimasi fungsi f(x,y) = 5 * x — 10 * y, maka panjang kromosomnya adalah 2, karena ada 2 variable yaitu x dan y yang akan kita cari nilainya. Contoh lain adalah jika kasusnya adalah Travelling Salesman Problem (TSP) maka panjang kromosomnya disesuaikan dengan jumlah tempat yang akan dikunjungi.

Selain itu, kita juga harus menentukan representasi kromosom yang akan digunakan. Ada beberapa representasi yang umum digunakan seperti representasi biner, integer, float, dan permutasi. Penentuan representasi disesuaikan dengan kasus yang akan diselesaikan.

Kita juga harus menentukan kapan proses algoritma genetika ini berhenti. Ada 2 cara yang umum digunakan, yang pertama adalah dengan menentukan threshold pada nilai fitness, yang kedua adalah dengan menentukan jumlah generasi.

Sebagai tambahan, kita juga harus menentukan nilai probabilitas crossover, dan probabilitas mutasi. Untuk alasannya, akan dijelaskan lebih lanjut seiring dengan proses yang akan saya jelaskan.

Perhitungan fitness

Setelah kita menginisialisasi populasi, maka langkah selanjutnya adalah menghitung nilai fitness untuk setiap kromosom. Fungsi fitness bisa bermacam-macam, tergantung masalah yang akan diselesaikan. Sebagai contoh, jika kita ingin mencari nilai maksimasi dari fungsi f(x,y) = 5 * x — 10 * y, maka cara menghitungnya adalah dengan memasukan nilai x dan y ke dalam fungsi tersebut.

Selection

Setelah memperoleh semua nilai fitness, proses selanjutnya adalah memilih orang tua. Tentukan jumlah orang tua yang akan dipilih lalu lakukan pemilihan dengan cara berikut. Terdapat beberapa cara untuk memilih kromosom orang tua.

1. Random Selection, memilih pasangan kromosom dari orang tua tanpa pengaruh dari nilai fitness. Sederhananya, hanya membangkitkan nilai random untuk memilih indeks dari kromosom orang tua.
2. Tournament Selection, metode seleksi ini membuat seleksi berdasarkan nilai fitness. Penyeleksian dimulai dengan memunculkan beberapa nilai sebagai indeks untuk memilih beberapa prospek orang tua, kemudian dipilih kromosom orang tua dengan fitness terbesar.
3. Roulette Wheel Selection, kegunaan dari metode seleksi ini berdasarkan probabilitas setiap kromosom. Ukuran proporsi dari kromosom di roulette wheel akan bervariasi tergantung nilai fitness. Penyeleksian dibuat dengan membangkitkan nilai random dari jarak semua nilai fitness.

Crossover

Setelah memilih orang tua, tahap selanjutnya kita akan melakukan crossover. Crossover adalah proses untuk membuat kromosom baru. Crossover dilakukan antara dua kromosom dan hasilnya adalah dua kromosom.

Ada dua pendekatan untuk menentukan kromosom baru, yaitu generational dan steady-state.

1. Generational. Menggunakan metode ini, kromosom baru dibuat sama dengan jumlah kromosom lama dan diakhir iterasi, populasi lama digantikan dengan populasi baru.
2. Steady-state. Tidak seperti metode generational, dalam steady-state, jumlah kromosom baru tidak sama dengan kromosom lama, tetapi hanya satu atau dua. Kromosom baru akan menggantikan kromosom lama.

Jika anda masih ingat, saat proses inisialisasi kita harus menentukan probabilitas crossover. Disinilah fungsi dari probabilitas tersebut. Probabilitas tersebut digunakan untuk menentukan apakah crossover terjadi atau tidak. Pada umumnya probabilitas crossover yang digunakan adalah 0,8, namun kita bebas menentukan probabilitas tersebut karena tidak ada kepastian mengenai probabilitas terbaik.

Kita harus membangkitkan nilai random dari rentang 0 sampai 1, jika nilai random lebih kecil atau sama dengan probabilitas crossover, maka crossover dilakukan. Adapun jenis crossover yang bisa dilakukan adalah sebagai berikut.

• One point crossover. Crossover ini mengganti gen dari satu kromosom untuk membuat kromosom baru dengan satu titik persimpangan.

• Multi-point crossover. Crossover ini mengganti gen dari satu kromosom untuk membuat kromosom baru dengan beberapa titik persimpangan.

• Uniform crossover. Crossover ini mengganti gen dari satu kromosom ke kromosom lain melalui setiap index berdasarkan probabilitas. Setiap gen mempunyai probabilitas seperti koin. Contohnya, jika kepala muncul maka akan diganti, dan jika ekor maka posisi akan tetap sama.

Semua titik potong tersebut didapatkan secara random.

Mutation

Hampir sama seperti crossover, mutasi tidak selalu dilakukan akibat adanya probabilitas mutasi. Probabilitas mutasi yang umum digunakan adalah 0,1. Sama seperti probabilitas crossover, tidak ada ketentuan yang pasti mengenai nilai dari probabilitas mutasi.

Pada prosesnya, mutasi mengubah fenotype dari gen (mengubah nilai gen). mutasi bisa dilakukan dengan satu titik atau juga bisa dengan banyak titik.

• One point mutation

• Multi-point mutation

• Swap mutation

Survivor selection

Selanjutnya adalah mendapatkan populasi lagi untuk iterasi berikutnya. Beberapa kromosom yang tidak penting akan dibuang dan digantikan dengan kromosom baru yang sudah melalui proses crossover dan mutasi.

Dalam penerapan algoritma genetika sebaiknya menggunakan prinsip Elitisme, yang mana selalu menyimpan satu kromosom terbaik selama proses sehingga akan selalu ada kromosom dengan fitness tertinggi. Jika muncul kombinasi kromosom terbaru yang lebih baik maka satu kromosom yang disimpan sebelumnya di tukar dengan kromosom baru tersebut.

Setelah menentukan populasi yang baru, proses selanjutnya adalah menghitung nilai fitness pada populasi yang baru. Hal tersebut akan terus berulang sampai dengan kondisi terminasi terpenuhi. Seperti yang telah dijelaskan sebelumnya, kondisi terminasi yang umum digunakan adalah dengan menggunakan threshold nilai fitness atau menentukan jumlah generasi maksimum.

Jika proses sudah berhenti, maka solusi dari algoritma genetika ini adalah kromosom dengan nilai fitness terbesar.